Most Magically Magical Magic Squares

In This Article
-
Magic squares are conspicuous instances of the intrinsic harmony of numbers. They are also noticeable instances of the inherent harmony of numbers that some consider as an interpreter of the cosmic order that dominates all existence. Can they?
-
Magic Squares are square grids with a unique arrangement of numbers in them. These numbers are exceptional because every row, column, and diagonal adds up to the same number.
-
Throughout history, humanity has been influenced by mathematics and numbers and has tried to reveal the unknowns by investigating the mysteries of numbers. Humanity’s long-time fascination with mathematics has arisen because the universe is constructed from a mathematical fabric.
No science teaches the harmonies of nature more clearly than mathematics. In arithmetic we explore a universe of figures by counting; in geometry we discover another universe by drawing lines and laying down definite directions in the conceptual field of the imagination; in algebra we produce magnitudes of a still more abstract nature that are expressed by letters. In all of these cases the first step is to establish the general conditions that lay down the rules which all further steps are subject to. Every one of these “universes” is dominated by a consistency that produces an excellent symmetry.
Certainly the world, the universe, and nature can be reliably understood using mathematics. In other words, we can say that nature is mathematics. For instance, the arrangement of seeds in a sunflower can be understood using Fibonacci numbers. Every number in the Fibonacci sequence equals the sum of the two previous except for the first two numbers. Sunflower heads, like other flowers, contain two families of interlaced spirals—one winding clockwise, the other counterclockwise. The shape assumed by a delicate spider web suspended from fixed points, or the cross section of sails bellying in the wind, is a catenary—a simple curve defined by a simple formula. Seashells, animal horns, and the cochlea of the ear are logarithmic spirals that can be generated using a mathematical constant known as the golden ratio. Mountains and the branching patterns of blood vessels and plants are fractals, a class of shapes that exhibit similar structures at different magnifications. Einstein’s E = mc2 defines the fundamental relationship between energy, matter, and the speed of light. Additionally, a few simple constants—the gravitational constant, Planck’s constant, and the speed of light—are profound examples for better understanding our universe as a whole.
Magic squares are conspicuous instances of the intrinsic harmony of numbers. They are also noticeable instances of the inherent harmony of numbers that some consider as an interpreter of the cosmic order that dominates all existence. Can they? Maybe. Though they are a mere intellectual play, they not only illustrate the nature of mathematics but also, incidentally, the nature of reality dominated by mathematical regularity. This is incidental, because its discovery has a very extraordinary story. Magic Squares are square grids with a unique arrangement of numbers in them. These numbers are exceptional because every row, column, and diagonal adds up to the same number. They are understood from every part in their overall square shape, the sum of which gives the same number – the sum of rows, columns, and diagonals. Magic Squares, one of the Sudoku-style question types, may vary in the numbers to be placed in the square according to its size. For example, let's say there is a 3x3 square and ask: how can you put the numbers 1 to 9 each in their own square so that all of the the rows, columns, and cross sums are always the same? I recommend you stop here for a while and work on the question. You can see that it is not as easy as it sounds. Otherwise, the answer is in Figure 1.
The historical development of magic squares is also very fascinating. The earliest record of magic squares is from China in about 2200 BC and is called Lo-Shu. It tells that the first magic square was incidentally discovered by the Chinese emperor Yu 4,200 years ago. Emperor Yu discovered a tortoise while sauntering along the Yellow River (Lo River). The tortoise's shell had a magic square shape, and this square divided into grids contained dots instead of numbers. Imagine having the same quantity as spots instead of numbers (Figure 2).
According to the myth, Emperor Yu took the tortoise and kept caring for it as a valuable guest in his palace. Its fame spread all over the world and extends beyond time to today's modern world. Perhaps, it deserves the title of the world's most famous mathematical tortoise with an outstanding mark on him. After the tortoise, the magic squares have become a very significant mystical symbol in China and in the Karma philosophy. In Karma, it is said that the world is surrounded by four essential elements and this is symbolized with magic squares. If we consider the number 5 in the center as the world, the followers of this philosophy surrounded the world with numbers that were supposed to be the four elements of Yin Yang. 4 and 9 symbolize metal, 2 and 7 symbolize fire, 1 and 6 symbolize water, and 3 and 8 signify wood, as shown in Figure 3.
We see that magic squares have mystical meanings not only in China but also in many places. For example, in pre-Islamic Arabia, people hung magic squares in their homes as amulets that they believe protected their houses from evil spirits. One explanation to this superstition could be that Arab astrologers used magic squares to cast horoscopes.
Magic squares were introduced to the Western world in the work of Theon of Smyrna. Theon’s most important work is “Expositio rerum mathematicarum ad legendum Platonem utilium.” This work is a handbook for philosophy students to show how prime numbers, geometrical numbers such as squares, progressions, music, and astronomy are interrelated. Its rather curious title means that it was intended as an introduction to a study of the works of Plato, which sounds rather fanciful. In the section on numbers, Theon adopts a Pythagorean approach and writes about all kinds of numbers: odd, even, prime, composite, square, oblong, triangular, polygonal, circular, spherical, solid numbers with three factors, pyramidal, perfect, deficient, and abundant numbers. The work of the Greek mathematician Moschopoulos in 1300 AD helped to spread knowledge about magic squares. So here we are now, more than 700 years later, and teachers are using them in class for problem-solving and practicing addition.
In the 16th century the Catholic physician, astrologer, and theologian Cornelius Agrippa (1486–1535) constructed squares of orders from 3, 4, 5, 6, 7, 8, and 9 which he associated with the seven known astrological planets: Saturn, Jupiter, Mars, the Sun, Venus, Mercury, and the Moon (the Sun and Moon were considered to be planets at that time.) Agrippa had a colorful life that included various dangerous run-ins with the Church and jobs as an occult scholar, lawyer, and military strategist. Agrippa’s De Occulta Philosophia stimulated Renaissance study of magic and got his name into early Faust legends. Agrippa believed that a magic square containing the digit 1—which exhibits the magic constant of 1 in all directions—represented God’s eternal perfection.
I do not think that anyone goes beyond the Indian people in terms of expecting help from magic squares for healing diseases and even finding a spouse. They also took first place in producing magic squares known as the Jaina inscriptions. The first 4x4 square was discovered on a door in Khajuraho, India, around 1100 AD (Figure 4). Jainism is an Indian philosophy that was established in the 6th century BC, which may imply how important magic squares are for Indians who follow this tradition.
India brought the usage of these squares to daily life. One superstition still practiced today is to write a 3x3 magic square to find someone missing and hang it everywhere like a notice. Strangely, the name of the missing person is not in the notice! The magic square’s merits are not limited to this. It is believed that a couple can save their marriage if they can get a copy of a square that is drawn on a Wednesday or Friday.
For mathematicians, it makes sense if the sums of squares across each row, column, or diagonal are equal. But Indians have different expectations from the squares. For example, the square used by young girls to get married is shown in Figure 5. This square is painted on a plate with pastels. The plate is washed in the Ganges River. The girl who is seeking her desired husband drinks the pastel-colored water from the river. This tradition is still being practiced today.
There are also squares used by Muslims in the Islamic period. One of the most beautiful examples of these squares is one designed to express God’s name as shown in Figure 6. The square with 66 letters in total on each side evokes the sum of the Arabic word Allah in Abjad calculation (In Arabic, every letter is assigned a numerical value, and this calculation is called Abjad).
Throughout history, humanity has been influenced by mathematics and numbers and has tried to reveal the unknowns by investigating the mysteries of numbers. Humanity’s long-time fascination with mathematics has arisen because the universe is constructed from a mathematical fabric. In 1623, Galileo Galilei reinforced this belief by stating his credo: “Nature’s great book is written in mathematical symbols.” Plato’s doctrine was that God is a geometer, and Sir James Jeans believed God experimented with arithmetic. Newton supposed that the planets were originally thrown into orbit by God, but even after God decreed the law of gravitation, the planets required continual adjustments to their orbits. Likewise, magic squares have been one such mysterious dimension of mathematics that have influenced human life in various ways.
|
4 |
9 |
2 |
|
3 |
5 |
7 |
|
8 |
1 |
6 |
Figure 1 – 3x3 Magic Square

Figure 2 - Spots on the tortoise
|
Metal 4 |
Metal 9 |
Fire 2 |
|
Wood 3 |
Earth 5 |
Fire 7 |
|
Wood 8 |
Water 1 |
Water 6 |
Figure 3 – Five Elements in Magic Square
|
7 |
12 |
1 |
14 |
|
2 |
13 |
8 |
11 |
|
16 |
3 |
10 |
5 |
|
9 |
6 |
15 |
4 |

Figure 4. Magic square at the Parshvanatha temple, Khajuraho
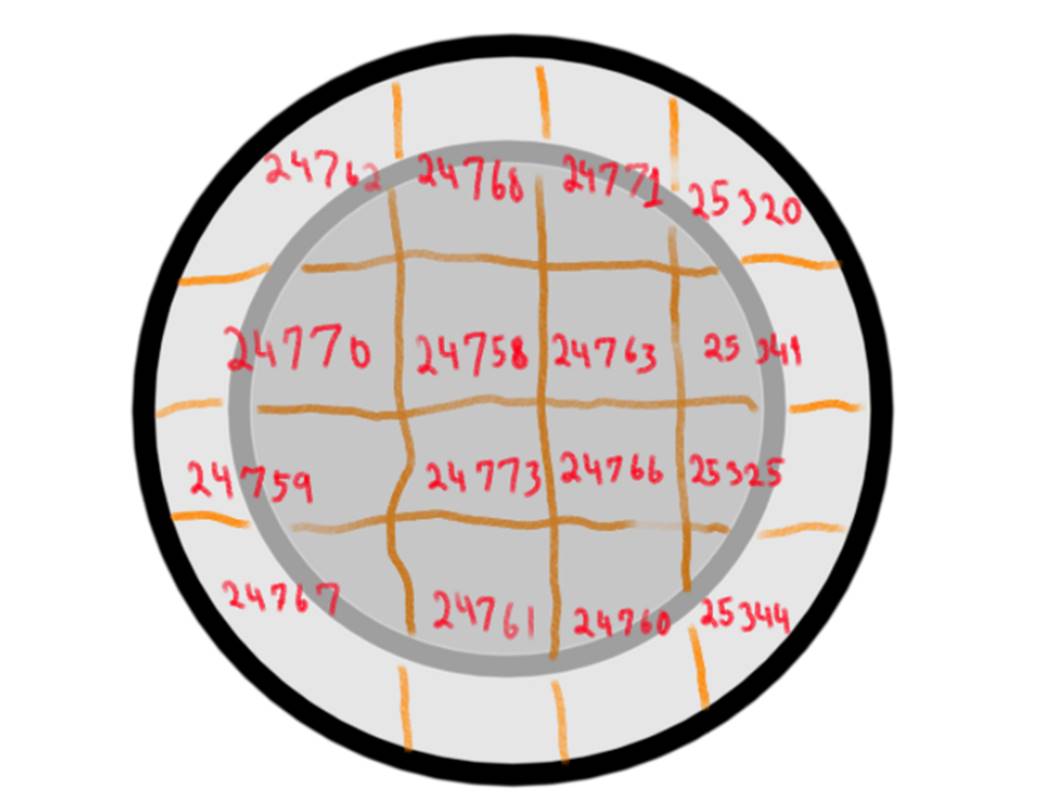
Figure 5 — Magic Square Drawn on a Plate with Pastel Paint
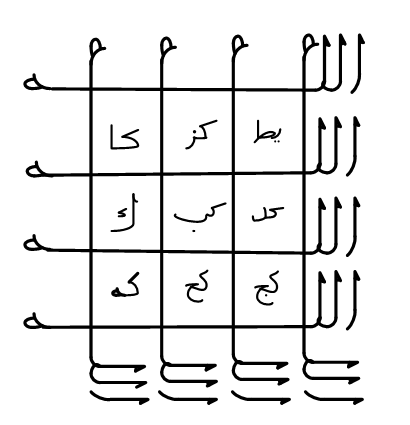
Figure 6- The sum of Allah's words with Abjad calculation is 66. The grid is formed by the letters in the word “Allah,” whose numerical value is also 66 (nineteenth century, Damascus).









